310. Minimum Height Trees

문제

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

예제 입출력

Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

참고

You can read the full description here.

책에 있는 풀이

참고

원본 코드는 여기에서 확인하실 수 있습니다.

풀이 1

접근법

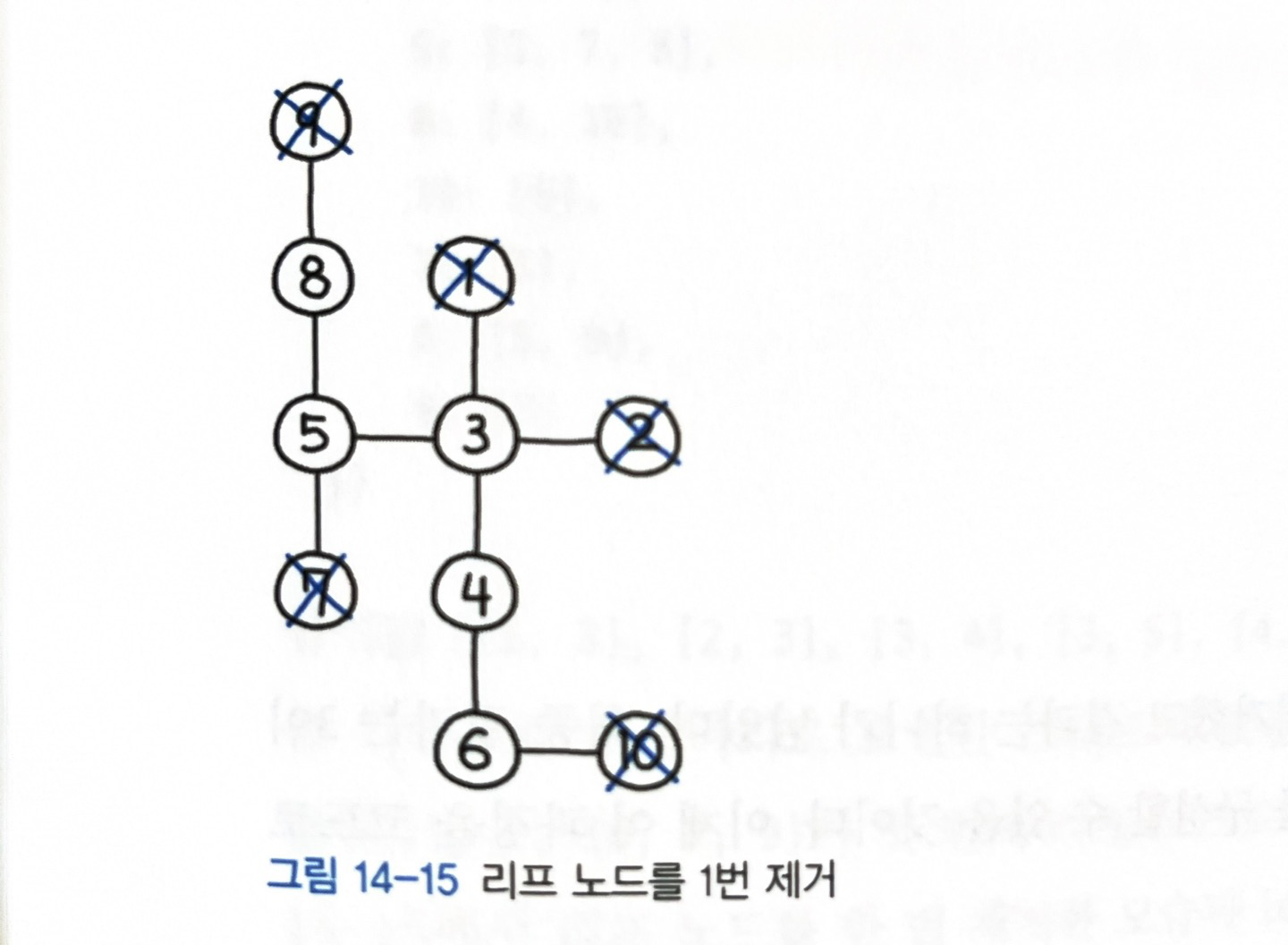
1. BFS로 접근합니다.
2. dictionary로 출발노드: [도착노드] 의 양방향 그래프를 구성합니다.
3. 값의 길이가 1개인 노드들을 leaf로 하고, 제거해줍니다.
4. 전체 노드가 2개 이하가 될 때까지 제거해줍니다.

구현 코드

import collections
from typing import List


# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None


class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        if n <= 1:
            return [0]

        # 양방향 그래프 구성
        graph = collections.defaultdict(list)
        for i, j in edges:
            graph[i].append(j)
            graph[j].append(i)

        # 첫 번째 리프 노드 추가
        leaves = []
        for i in range(n + 1):
            if len(graph[i]) == 1:
                leaves.append(i)

        # 루트 노드만 남을 때까지 반복 제거
        while n > 2:
            n -= len(leaves)
            new_leaves = []
            for leaf in leaves:
                neighbor = graph[leaf].pop()
                graph[neighbor].remove(leaf)

                if len(graph[neighbor]) == 1:
                    new_leaves.append(neighbor)

            leaves = new_leaves

        return leaves